Time and Location

Time: TBD
Zoom Link: Please use the link on KDD virtual platform

Abstract

Graph Neural Networks (GNNs) and differential equations (DEs) are two rapidly advancing areas of research that have shown remarkable synergy in recent years. GNNs have emerged as powerful tools for learning on graph-structured data, while differential equations provide a principled framework for modeling continuous dynamics across time and space. The intersection of these fields has led to innovative approaches that leverage the strengths of both, enabling applications in physics-informed learning, spatiotemporal modeling, and scientific computing. This survey aims to provide a comprehensive overview of the burgeoning research at the intersection of GNNs and DEs. We categorize existing methods, discuss their underlying principles, and highlight their applications across domains such as molecular modeling, traffic prediction, and epidemic spreading. Furthermore, we identify open challenges and outline future research directions to advance this interdisciplinary field. A comprehensive list of related papers is available at: https://github.com/Emory-Melody/Awesome-Graph-NDEs. This survey serves as a resource for researchers and practitioners seeking to understand and contribute to the fusion of GNNs and DEs.

Target Audience

This tutorial targets researchers and practitioners from graph machine learning, dynamical systems modeling, and interdisciplinary scientific communities interested in Graph Neural Differential Equations. Participants are recommended to have foundational knowledge of differential equations, (un)supervised learning, neural networks, and basic concepts of graph learning. Prior experience with training GNN models will be advantageous.

Tutorial Syllabus

The topics of this full-day tutorial include (but are not limited to) the following:

• Fundamentals of dynamical systems, differential equations, and graph neural networks
• Neural Differential Equations: ODEs, PDEs, and SDEs
• Integration of GNNs with differential equations
• Taxonomies and modeling methodologies of Graph Neural Differential Equations (Graph NDEs)
• Spatial and temporal dynamics in graph-structured systems
• In-depth analysis of challenges and solutions in Graph NDEs
• Real-world applications: physics simulations, traffic forecasting, epidemic modeling, and recommender systems
• Open challenges and future research directions in Graph NDEs

The tutorial outline is shown below:

1. Introduction and Background (30 minutes)

   1. Dynamical Systems and Differential Equations

   2. Neural Differential Equations

   3. Learning on Graphs and Graph Neural Networks

2. Taxonomies and Methodologies of Graph NDEs (30 minutes)

   1. Roles of GNNs

   2. Graph Construction

   3. Modeling Spatial & Temporal Dynamics

3. Break (20 minutes)

4. In-depth Exploration of Graph NDE Models (60 minutes)

   1. Challenges and Solutions for Spatial Dynamics

   2. Challenges and Solutions for Temporal Dynamics

5. Applications and Future Directions (40 minutes)

The detailed tutorial outline is shown below:

Introduction and Background: This section covers essential concepts required to understand the tutorial, including dynamical systems, differential equations, and foundational aspects of GNNs.

Taxonomies and Methodologies of Graph NDEs: We provide a structured taxonomy of Graph NDEs, detailing their types, roles, and methodologies.

• Neural Differential Equations: Introducing various Neural Differential Equations integrated with ODEs, PDEs, and SDEs, and summarizing their characteristics, strengths, and limitations in modeling complex dynamical systems.
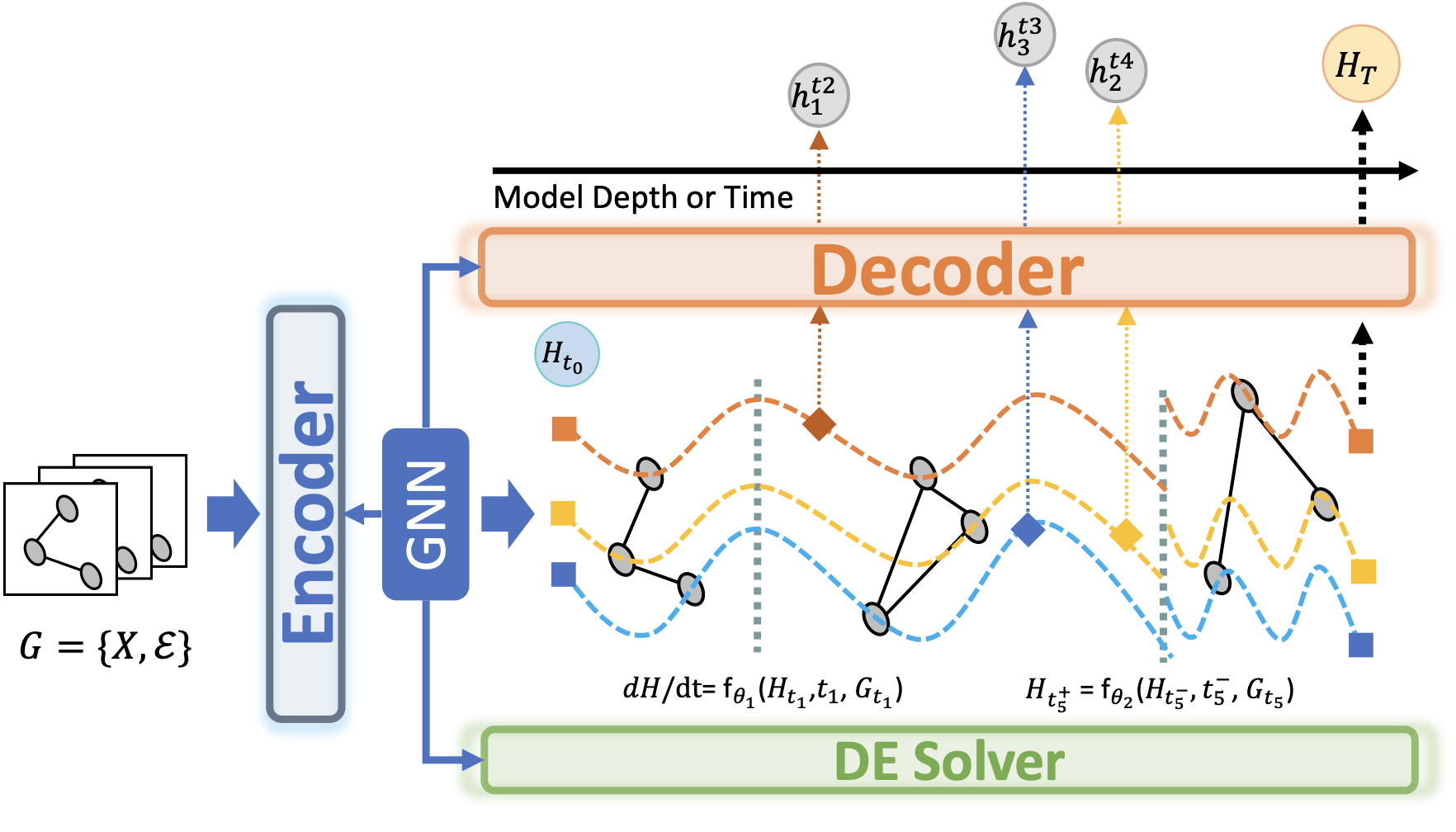
• Roles of Graph Neural Networks: This subsection categorizes the roles of GNNs within the framework of Graph NDEs, specifically detailing their functions as encoders, decoders, and direct parameterizations of the differential equations. We also categorize the methods for constructing the initial condition for the differential equations to solve, including encoding-based, pre-defined, and learning-based methods, emphasizing their relevance to system modeling effectiveness.
• Graph Construction: Discusses different strategies of graph construction, spanning both spatial and temporal levels.

In-depth Exploration of Graph NDE Models: We introduce various approaches for integrating Graph Neural Networks with Neural Differential Equations, and how they address some classic challenges in the domain of GNNs and DEs.

Applications in Real-world Scenarios: Examination of real-world scenarios where Graph NDEs significantly improve modeling outcomes across domains such as epidemiology, physical systems, traffic flow, and recommendation systems.

Future Directions and Conclusions: Highlighting emerging research avenues, we address the need in the modeling of multi-scale data, continuous structural dynamics, equation discovery, sparse data, and large-scale systems.

Presenters